数据结构与算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


#include "stdafx.h"

//void PrintN(int N)
//{
//int i;
//for (i = 1; i <= N; i++){
//printf("%d\n", i);
//}
//return;
//}
void PrintN(int N)
{
	if (N){
		PrintN(N - 1);
		printf("%d\n", N);
	}
	return;
}

int main()
{
	int N;
	scanf_s("%d", &N);
	PrintN(N);
	return 0;
}

关于空间使用

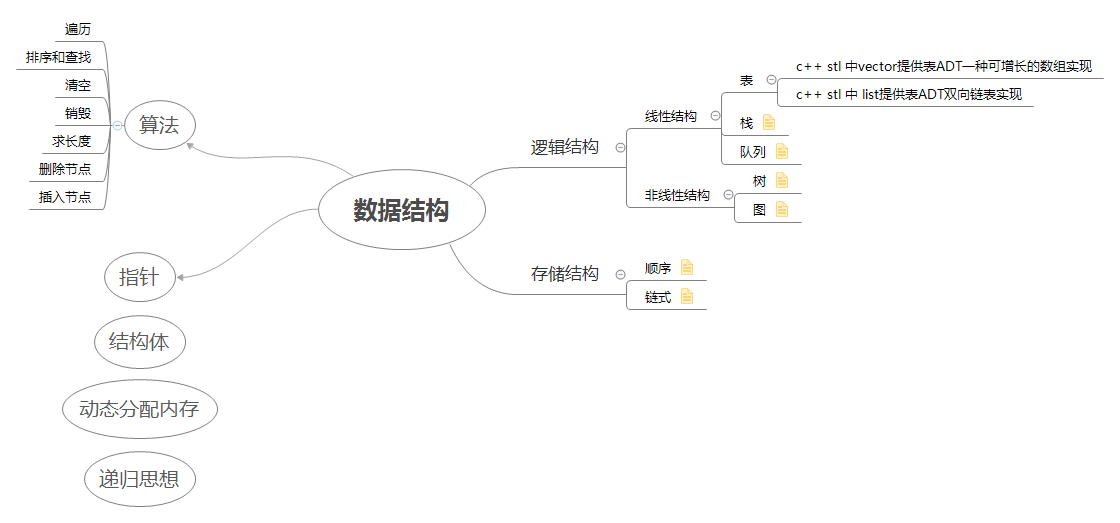
数据结构概述

定义
我们如何把现实中大量而反复的问题以特定的数据类型和特定的存储结构保存到主存储器(内存)中，以及在此基础上为实现某个功能（比如查找某个元素，删除某个元素，对所有元素进行排序）而执行的相应的操作，这个相应的操作也叫做算法。
数据结构=个体+个体的关系
算法=对存储数据的操作
狭义：
数据结构是专门研究数据存储的问题
数据的存储包含两方面：个体的存储 + 个体关系的存储
广义：
数据结构既包含数据的存储也包含数据的操作对存储数据的操作就是算法

算法概述

狭义：
算法是和数据的存储方式密切相关
广义：
算法和数据的存储方式无关，这就是泛型思想
衡量算法的标准：
（1）时间复杂度
大概程序要执行的次数，而并非是执行的时间（因为同一程序在不同机器上执行的时间是不一样的，有差异）
（2）空间复杂度
算法执行过程中大概所占用的最大内存
（3）难易程度
（4）健壮性

指针

1
2
3
4
5
6


int i=10;           int* i=10

int *p = &i;        int* *p=&i;
//等价于            //等价于
int *p;             int* *p;
p = &i;             *p=&i;

详解这两部操作：
1）、p存放了i的地址，所以我们说p指向了i
2）、p和i是完全不同的两个变量，修改其中的任意一个变量的值，不会影响另一变量的值
3）、p指向i，*p 就是i变量本身。更形象的说所有出现 *p 的地方都可以换成i，所有出现i的地方都可以换成 *p

指针和一维数组
数组名
一维数组名是个指针常量，
它存放的是一维数组第一个元素的地址，
它的值不能被改变
一维数组名指向的是数组的第一个元素

下标和指针的关系
a[i] <<==>> * (a+i)
假设指针变量的名字为p
则p+i的值是p+i*(p所指向的变量所占的字节数)

指针变量的运算
指针变量不能相加，不能相乘，不能相除
如果两指针变量属于同一数组，则可以相减
指针变量可以加减一整数，前提是最终结果不能超过指针允许指向的范围
p+i的值是p+i(p所指向的变量所占的字节数)
p-i的值是p-i(p所指向的变量所占的字节数)
p++ <==>p+1
p– <==> p-1

结构体

结构体（C++中用类也能实现）

为什么会出现结构体
为了表示一些复杂的数据，而普通的基本类型变量无法满足要求
什么叫结构体
结构体是用户根据实际需要自己定义的复合数据类型

如何使用结构体
两种方式：

1
2
3
4


struct Student st = {1000, "zhangsan", 20}  
struct Student * pst = &st;
1.  st.sid  
2.  pst->sid

pst所指向的结构体变量中的sid这个成员

注意事项：
结构体变量不能加减乘除，但可以相互赋值
普通结构体变量和结构体指针变量作为函数参数的传递

动态分配内存

1

int * pArr = (int *)malloc(sizeof(int) * len);

(int *) 的解释无论变量占几个字节它都是以第一个字节来表示，此处的(int *)就代表malloc 返回的就不是一个没有意义的地址了而是一个4个字节的整型地址。(这里的强制转换相当于告诉编译器我们返回的到底是整型还是浮点型)

跨函数使用内存问题

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


main()
{
	int *p;
	fun(&p);
	…
}
int fun(int **q)
{
	int s;
	*q = &s;

这里主函数调用fun函数为期局部变量s分配内存，单调用结束这块内存就没有了，指针p 就变成了野指针。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


#include <stdlib.h>
main()
{
	int *p;
	fun(&p);   //*q=&p
	…
}
int fun(int* *q)
{
	*q = (int *)malloc(4);
}

int* 类型的变量p发送地址给 int* 类型的指针变量q 这时*q 就是p 的内容了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


# include <stdio.h>
# include <malloc.h>

struct Student
{
	int sid;
	int age;
};

struct Student * CreateStudent(void);
void ShowStudent(struct Student *);

int main(void)
{
	struct Student * ps;

	ps = CreateStudent();
	ShowStudent(ps);

	return 0;
}

void ShowStudent(struct Student * pst)
{
	printf("%d %d\n", pst->sid, pst->age);
}

struct Student * CreateStudent(void)
{
	struct Student * p = (struct Student *)malloc(sizeof(struct Student));
	p->sid = 99;
	p->age = 88;
	return p;
}

这是一个跨函数使用内存的例子

一点思考面向过程面向象的函数区别也就是c 与c++的函数区别？存储不一样操作不一样，泛型存储不一样操作也一样。

线性结构表

顺序存储 [数组]

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202


# include <stdio.h>
# include <malloc.h>  //包含了malloc函数
# include <stdlib.h>  //包含了exit函数

//定义了一个数据类型，该数据类型的名字叫做struct Arr, 该数据类型含有三个成员，分别是pBase, len, cnt
struct Arr
{
	int * pBase; //存储的是数组第一个元素的地址
	int len; //数组所能容纳的最大元素的个数
	int cnt; //当前数组有效元素的个数
};

void init_arr(struct Arr * pArr, int length);  //分号不能省
bool append_arr(struct Arr * pArr, int val); //追加
bool insert_arr(struct Arr * pArr, int pos, int val); // pos的值从1开始
bool delete_arr(struct Arr * pArr, int pos, int * pVal);
int get();
bool is_empty(struct Arr * pArr);
bool is_full(struct Arr * pArr);
void sort_arr(struct Arr * pArr);
void show_arr(struct Arr * pArr);
void inversion_arr(struct Arr * pArr);

int main(void)
{
	struct Arr arr;
	int val;

	init_arr(&arr, 6);
	show_arr(&arr);
	append_arr(&arr, 1);
	append_arr(&arr, 10);
	append_arr(&arr, -3);
	append_arr(&arr, 6);
	append_arr(&arr, 88);
	append_arr(&arr, 11);
	if (delete_arr(&arr, 4, &val))
	{
		printf("删除成功!\n");
		printf("您删除的元素是: %d\n", val);
	}
	else
	{
		printf("删除失败!\n");
	}
	/*append_arr(&arr, 2);
	append_arr(&arr, 3);
	append_arr(&arr, 4);
	append_arr(&arr, 5);
	insert_arr(&arr, -1, 99);
	append_arr(&arr, 6);
	append_arr(&arr, 7);
	if ( append_arr(&arr, 8) )
	{
	printf("追加成功\n");
	}
	else
	{
	printf("追加失败!\n");
	}
	*/
	show_arr(&arr);
	inversion_arr(&arr);
	printf("倒置之后的数组内容是:\n");
	show_arr(&arr);
	sort_arr(&arr);
	show_arr(&arr);

	//printf("%d\n", arr.len);

	return 0;
}

void init_arr(struct Arr * pArr, int length)
{
	pArr->pBase = (int *)malloc(sizeof(int) * length);
	if (NULL == pArr->pBase)
	{
		printf("动态内存分配失败!\n");
		exit(-1); //终止整个程序
	}
	else
	{
		pArr->len = length;
		pArr->cnt = 0;
	}
	return;
}

bool is_empty(struct Arr * pArr)
{
	if (0 == pArr->cnt)
		return true;
	else
		return false;
}

bool is_full(struct Arr * pArr)
{
	if (pArr->cnt == pArr->len)
		return true;
	else
		return false;
}

void show_arr(struct Arr * pArr)
{
	if (is_empty(pArr))
	{
		printf("数组为空!\n");
	}
	else
	{
		for (int i = 0; i < pArr->cnt; ++i)
			printf("%d  ", pArr->pBase[i]); //int *
		printf("\n");
	}
}

bool append_arr(struct Arr * pArr, int val)
{
	//满是返回false
	if (is_full(pArr))
		return false;

	//不满时追加
	pArr->pBase[pArr->cnt] = val;
	(pArr->cnt)++;
	return true;
}

bool insert_arr(struct Arr * pArr, int pos, int val)
{
	int i;

	if (is_full(pArr))
		return false;

	if (pos<1 || pos>pArr->cnt + 1)  //
		return false;

	for (i = pArr->cnt - 1; i >= pos - 1; --i)
	{
		pArr->pBase[i + 1] = pArr->pBase[i];
	}
	pArr->pBase[pos - 1] = val;
	(pArr->cnt)++;
	return true;
}

bool delete_arr(struct Arr * pArr, int pos, int * pVal)
{
	int i;

	if (is_empty(pArr))
		return false;
	if (pos<1 || pos>pArr->cnt)
		return false;

	*pVal = pArr->pBase[pos - 1];
	for (i = pos; i < pArr->cnt; ++i)
	{
		pArr->pBase[i - 1] = pArr->pBase[i];
	}
	pArr->cnt--;
	return true;
}

void inversion_arr(struct Arr * pArr)
{
	int i = 0;
	int j = pArr->cnt - 1;
	int t;

	while (i < j)
	{
		t = pArr->pBase[i];
		pArr->pBase[i] = pArr->pBase[j];
		pArr->pBase[j] = t;
		++i;
		--j;
	}
	return;
}

void sort_arr(struct Arr * pArr)
{
	int i, j, t;

	for (i = 0; i < pArr->cnt; ++i)
	{
		for (j = i + 1; j < pArr->cnt; ++j)
		{
			if (pArr->pBase[i] > pArr->pBase[j])
			{
				t = pArr->pBase[i];
				pArr->pBase[i] = pArr->pBase[j];
				pArr->pBase[j] = t;
			}
		}
	}
}

冒泡排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53


//#include<stdio.h>
//#include "stdafx.h"
//#include<iostream>
//#include<fstream>
//#include<cstring>
//using namespace std;

void main()
{
	int n = 9;
	int a[9] = { 2, 1, 3, 5, 2, 9, 0, 150, 11 };
	for (int i = 0; i < n; i++)
		for (int j = i; j < n; ++j)
			if (a[i] > a[j])
			{
				int temp = a[i];
				a[i] = a[j];
				a[j] = temp;
			}
	/*for (int x = 0; x < n; ++x)
	cout << a[x] << " ";*/
	for (int i = 0; i < n; ++i)
		printf("%d  ", a[i]);


}
//数组冒泡排序元素
//法一：for(int i = counter - 1; i > 0; i--)
//for (int j = 0; j <= i; j++)
//if (elem[j] > elem[i])
//{
//int temp = elem[j];
//elem[j] = elem[i];
//elem[i] = temp;
//
//}
//
//法二：for(int i = 0; i < counter; i++)
//for (int j = counter - 1; j > i; j--)
//if (elem[i] > elem[j])
//{
//int temp = elem[i];
//elem[i] = elem[j];
//elem[j] = temp;
//}
//法三：for(int i = 0; i < counter; ++i)
//for (int j = i; j <counter; ++j)
//if (elem[i] > elem[j])
//{
//int temp = elem[i];
//elem[i] = elem[j];
//elem[j] = temp;
//}

链式存储 [链表]

非循环单链表

1
2


r = p->pNext; p->pNext = q;  q->pNext = r;  
q->pNext = p->pNext;  p->pNext = q;用赋值 和 指针域等于下一结点的地址思想去理解 

插入节点

1
2
3


r = p->pNext;
p->pNext = r->pNext;
free(r); 用赋值 和 指针域等于下一结点的地址思想去理解 

删除节点

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217


# include <stdio.h>
# include <malloc.h>
# include <stdlib.h>

typedef struct Node
{
	int data; //数据域
	struct Node * pNext; //指针域
}NODE, *PNODE; //NODE等价于struct Node    PNODE等价于struct Node *

//函数声明
PNODE create_list(void);  //创建链表
void traverse_list(PNODE pHead);  //遍历链表
bool is_empty(PNODE pHead);  //判断链表是否为空
int length_list(PNODE);  //求链表长度
bool insert_list(PNODE pHead, int pos, int val);  //在pHead所指向链表的第pos个节点的前面插入一个新的结点，该节点的值是val， 并且pos的值是从1开始
bool delete_list(PNODE pHead, int pos, int * pVal);  //删除链表第pos个节点，并将删除的结点的值存入pVal所指向的变量中,  并且pos的值是从1开始
void sort_list(PNODE);  //对链表进行排序


int main(void)
{
	PNODE pHead = NULL; //等价于 struct Node * pHead = NULL;
	int val;

	pHead = create_list();  //create_list()功能：创建一个非循环单链表，并将该链表的头结点的地址付给pHead
	traverse_list(pHead);

	//insert_list(pHead, -4, 33);
	if (delete_list(pHead, 4, &val))
	{
		printf("删除成功，您删除的元素是: %d\n", val);
	}
	else
	{
		printf("删除失败!您删除的元素不存在!\n");
	}

	traverse_list(pHead);

	//int len = length_list(pHead);
	//printf("链表的长度是%d\n", len);

	//sort_list(pHead);
	//traverse_list(pHead);

	/*if ( is_empty(pHead) )
	printf("链表为空!\n");
	else
	printf("链表不空!\n");
	*/
	return 0;
}

PNODE create_list(void)
{
	int len;  //用来存放有效节点的个数
	int i;
	int val; //用来临时存放用户输入的结点的值

	//分配了一个不存放有效数据的头结点
	PNODE pHead = (PNODE)malloc(sizeof(NODE));
	if (NULL == pHead)
	{
		printf("分配失败, 程序终止!\n");
		exit(-1);
	}
	PNODE pTail = pHead;
	pTail->pNext = NULL;

	printf("请输入您需要生成的链表节点的个数: len = ");
	scanf("%d", &len);

	for (i = 0; i < len; ++i)
	{
		printf("请输入第%d个节点的值: ", i + 1);
		scanf("%d", &val);

		PNODE pNew = (PNODE)malloc(sizeof(NODE));
		if (NULL == pNew)
		{
			printf("分配失败, 程序终止!\n");
			exit(-1);
		}
		pNew->data = val;
		pTail->pNext = pNew;
		pNew->pNext = NULL;
		pTail = pNew;
	}

	return pHead;
}

void traverse_list(PNODE pHead)
{
	PNODE p = pHead->pNext;

	while (NULL != p)
	{
		printf("%d  ", p->data);
		p = p->pNext;
	}
	printf("\n");

	return;
}

bool is_empty(PNODE pHead)
{
	if (NULL == pHead->pNext)
		return true;
	else
		return false;
}

int length_list(PNODE pHead)
{
	PNODE p = pHead->pNext;
	int len = 0;

	while (NULL != p)
	{
		++len;
		p = p->pNext;
	}

	return len;
}

void sort_list(PNODE pHead)
{
	int i, j, t;
	int len = length_list(pHead);
	PNODE p, q;

	for (i = 0, p = pHead->pNext; i < len - 1; ++i, p = p->pNext)
	{
		for (j = i + 1, q = p->pNext; j < len; ++j, q = q->pNext)
		{
			if (p->data > q->data)  //类似于数组中的:  a[i] > a[j]
			{
				t = p->data;//类似于数组中的:  t = a[i];
				p->data = q->data; //类似于数组中的:  a[i] = a[j];
				q->data = t; //类似于数组中的:  a[j] = t;
			}
		}
	}

	return;
}

//在pHead所指向链表的第pos个节点的前面插入一个新的结点，该节点的值是val， 并且pos的值是从1开始
bool insert_list(PNODE pHead, int pos, int val)
{
	int i = 0;
	PNODE p = pHead;

	while (NULL != p && i < pos - 1)
	{
		p = p->pNext;
		++i;
	}

	if (i > pos - 1 || NULL == p)
		return false;

	//如果程序能执行到这一行说明p已经指向了第pos-1个结点,但第pos-1个节点是否存在无所谓
	//分配新的结点
	PNODE pNew = (PNODE)malloc(sizeof(NODE));
	if (NULL == pNew)
	{
		printf("动态分配内存失败!\n");
		exit(-1);
	}
	pNew->data = val;

	//将新的结点存入p节点的后面
	PNODE q = p->pNext;
	p->pNext = pNew;
	pNew->pNext = q;

	//法二
	//pNew->pNext = p->pNext;
	//p->pNext = pNew;

	return true;
}


bool delete_list(PNODE pHead, int pos, int * pVal)
{
	int i = 0;
	PNODE p = pHead;

	while (NULL != p->pNext && i < pos - 1)
	{
		p = p->pNext;
		++i;
	}//让p指向了第pos-1个结点

	if (i > pos - 1 || NULL == p->pNext)
		return false;

	//如果程序能执行到这一行说明p已经指向了第pos-1个结点，并且第pos个节点是存在的
	PNODE q = p->pNext;  //q指向待删除的结点
	*pVal = q->data;

	//删除p节点后面的结点
	p->pNext = p->pNext->pNext;//等价于 p->pNext = q->PNext;

	//释放q所指向的节点所占的内存
	free(q);
	q = NULL;

	return true;

}

顺序存储与链式存储优缺点

顺序存储
优点：
存取速度快因为直接定为某个位置
缺点：
事先必须知道数组的长度
插入删除元素很慢
空间通常是有限的
需要大块连续的内存块

链式存储
优点：
空间没有限制
插入删除元素很快
缺点：
存取速度很慢因为要定位到某个结点要去遍历

线性结构的应用–栈

静态分配内存（局部变量）—栈一种“先进后出”的存储结构
动态分配内存（malloc new )—堆顺序随意
栈又分静态栈（功能受限顺序存储）动态栈（功能受限链式存储）

静态栈

动态栈（重点）

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141


# include <stdio.h>
# include <malloc.h>
# include <stdlib.h>

typedef struct Node
{
	int data;
	struct Node * pNext;
}NODE, *PNODE;

typedef struct Stack
{
	PNODE pTop;
	PNODE pBottom;
}STACK, *PSTACK;  //PSTACK 等价于 struct STACK *

void init(PSTACK);
void push(PSTACK, int);
void traverse(PSTACK);
bool pop(PSTACK, int *);
void clear(PSTACK pS);

int main(void)
{
	STACK S;  //STACK 等价于 struct Stack
	int val;

	init(&S);  //目的是造出一个空栈
	push(&S, 1); //压栈
	push(&S, 2);
	push(&S, 3);
	push(&S, 4);
	push(&S, 5);
	push(&S, 6);
	traverse(&S); //遍历输出

	clear(&S);
	//traverse(&S); //遍历输出

	if (pop(&S, &val))
	{
		printf("出栈成功，出栈的元素是%d\n", val);
	}
	else
	{
		printf("出栈失败!\n");
	}

	traverse(&S); //遍历输出

	return 0;
}

void init(PSTACK pS)
{
	pS->pTop = (PNODE)malloc(sizeof(NODE));
	if (NULL == pS->pTop)
	{
		printf("动态内存分配失败!\n");
		exit(-1);
	}
	else
	{
		pS->pBottom = pS->pTop;
		pS->pTop->pNext = NULL; //pS->Bottom->pNext = NULL;
	}
}

void push(PSTACK pS, int val)
{
	PNODE pNew = (PNODE)malloc(sizeof(NODE));

	pNew->data = val;
	pNew->pNext = pS->pTop; //pS->Top不能改成pS->Bottom
	pS->pTop = pNew;

	return;
}

void traverse(PSTACK pS)
{
	PNODE p = pS->pTop;

	while (p != pS->pBottom)
	{
		printf("%d  ", p->data);
		p = p->pNext;
	}
	printf("\n");

	return;
}

bool empty(PSTACK pS)
{
	if (pS->pTop == pS->pBottom)
		return true;
	else
		return false;
}

//把pS所指向的栈出栈一次，并把出栈的元素存入pVal形参所指向的变量中，如果出栈失败，返回false,否则返回true
bool pop(PSTACK pS, int * pVal)
{
	if (empty(pS)) //pS本身存放的就是S的地址
	{
		return false;
	}
	else
	{
		PNODE r = pS->pTop;
		*pVal = r->data;
		pS->pTop = r->pNext;
		free(r);
		r = NULL;

		return true;
	}
}

//clear清空
void clear(PSTACK pS)
{
	if (empty(pS))
	{
		return;
	}
	else
	{
		PNODE p = pS->pTop;
		PNODE q = NULL;

		while (p != pS->pBottom)
		{
			q = p->pNext;
			free(p);
			p = q;
		}
		pS->pTop = pS->pBottom;
	}
}

算法（往里放，从里取）
出栈
压栈
应用
函数调用
中断
表达式求值（用两个栈，一个存放数字，一个存放符号）
内存分配
缓冲处理
迷宫

线性结构的应用–队列

定义：一种可是实现“先进先出”的存储结构
分类：
链式队列：用链表实现
静态队列(用循环队列）：用数组实现

动态队列

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112


# include <iostream>
using namespace std;

typedef struct node
{
	int data;
	struct node *pNext;
}NODE, *PNODE;

class Queue
{
public:
	Queue()
	{
		this->pHead = this->pTail = new NODE;
		this->pHead->pNext = NULL;
	}

	void InQueue(int val)
	{
		PNODE pNew = new NODE;

		pNew->data = val;
		pNew->pNext = NULL;

		pTail->pNext = pNew; //将pNew挂到队列尾部 
		pTail = pNew; //注意是尾指针上移

		return;
	}

	bool Empty() const
	{
		if (this->pHead == pTail)
			return true;
		else
			return false;
	}

	int OutQueue()
	{
		if (Empty())
		{
			cout << "队列为空，无法出队!" << endl;
		}
		else
		{
			PNODE pTemp = pHead->pNext; //pHead不是要删除的队首元素，pHead->pNext所指向的元素才是要删除的元素，
			pHead->pNext = pTemp->pNext;
			int val = pTemp->data;

			delete pTemp;

			if (NULL == pHead->pNext) //如果队列为空
			{
				pTail = pHead; //尾指针也指向无用的头结点
			}

			return val;
		}
	}

	//遍历队列
	void Travers(void) const
	{
		PNODE pTemp = pHead->pNext;

		while (pTemp != NULL)
		{
			cout << pTemp->data << "  ";
			pTemp = pTemp->pNext;
		}
		cout << endl;
	}

	void Clear()
	{
		while (!this->Empty())
		{
			OutQueue();
		}
	}

	~Queue()
	{
		this->Clear();
		delete pHead;
	}

private:
	PNODE pHead, pTail; //pHead指向无用的头结点 pHead->pNext才是指向队首元素， pTail指向队尾元素
};

int main(void)
{
	Queue Q;

	for (int i = 0; i < 5; ++i)
		Q.InQueue(i + 1);

	Q.Travers();

	Q.OutQueue();
	Q.OutQueue();

	Q.Travers();

	Q.Clear();
	Q.OutQueue();

	return 0;
}

静态队列（重点）

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113


# include <stdio.h>
# include <malloc.h>

typedef struct Queue
{
	int * pBase;
	int front;
	int rear;
}QUEUE;

void init(QUEUE *);
bool en_queue(QUEUE *, int val);  //入队
void traverse_queue(QUEUE *);
bool full_queue(QUEUE *);
bool out_queue(QUEUE *, int *);
bool emput_queue(QUEUE *);

int main(void)
{
	QUEUE Q;
	int val;

	init(&Q);
	en_queue(&Q, 1);
	en_queue(&Q, 2);
	en_queue(&Q, 3);
	en_queue(&Q, 4);
	en_queue(&Q, 5);
	en_queue(&Q, 6);
	en_queue(&Q, 7);
	en_queue(&Q, 8);

	traverse_queue(&Q);

	if (out_queue(&Q, &val))
	{
		printf("出队成功，队列出队的元素是: %d\n", val);
	}
	else
	{
		printf("出队失败!\n");
	}
	traverse_queue(&Q);

	return 0;
}

void init(QUEUE *pQ)
{
	pQ->pBase = (int *)malloc(sizeof(int) * 6);
	pQ->front = 0;
	pQ->rear = 0;
}

bool full_queue(QUEUE * pQ)
{
	if ((pQ->rear + 1) % 6 == pQ->front)
		return true;
	else
		return false;
}

bool en_queue(QUEUE * pQ, int val)
{
	if (full_queue(pQ))
	{
		return false;
	}
	else
	{
		pQ->pBase[pQ->rear] = val;
		pQ->rear = (pQ->rear + 1) % 6;

		return true;
	}
}

void traverse_queue(QUEUE * pQ)
{
	int i = pQ->front;

	while (i != pQ->rear)
	{
		printf("%d  ", pQ->pBase[i]);
		i = (i + 1) % 6;
	}
	printf("\n");

	return;
}

bool emput_queue(QUEUE * pQ)
{
	if (pQ->front == pQ->rear)
		return true;
	else
		return false;
}

bool out_queue(QUEUE * pQ, int * pVal)
{
	if (emput_queue(pQ))
	{
		return false;
	}
	else
	{
		*pVal = pQ->pBase[pQ->front];
		pQ->front = (pQ->front + 1) % 6;

		return true;
	}
}

循环队列的讲解
(1)静态队列为什么必须是循环队列
一直增增删删，那么就会造成rear端溢出，而front端浪费，所以对于这种情况，可以采用循环队列的形式，即当rear已经指向数组最后一个元素时，那么就可以转而将rear指向数组的第一个空出来的空间。
(2）循环队列需要几个参数来确定
需要2个参数来确定：front 和 rear
(3)循环队列各个参数的含义：
2个参数在不同场合有不同的含义
队列初始化
front和rear的值都为零
队列非空
front代表的是队列的第一个元素
rear代表的是队列的最后一个有效元素的下一个元素
队列为空
front和real的值相等，但不一定为零
(4)循环队列入队伪算法讲解：
两步完成：
将值存入rear所代表的位置
错误的写法：rear = rear+1;
正确的写法是：rear = (rear+1)%数组的长度
(5)循环队列出队伪算法讲解
Front =（front +1）%数组的长度
(6)如何判断循环队列是否为空
如果front与rear的值相等，则该队列就一定为空
(7)如何判断循环队列是否已满
因为front的值可能比rear大，也可能比他小，也可能相等
所以有两种方式:
多增加一个标识是否满的参数
少用一个元素【通常用此种方式】
如果front和rear的值相差1，且front>rear,则证明队列已满。
用C语言伪算法表示为：
if ((rear+1)%数组长度==front)
已满
else
未满

递归

函数的调用
当在一个函数的运行期间调用另一个函数时，在运行被调函数之前，系统需要完成三件事：
将所有的实际参数，返回地址等信息传递给被调函数。
为被调函数的局部变量（也包括形参）分配存储空间
将控制转移到被调函数的入口
从被调函数返回主调函数之前，系统也要完成三件事：
保存被调函数的返回结果
释放被调函数所占的存储空间
依照被调函数保存的返回地址将控制转移到调用函数
递归和循环的优缺点比较
递归：
易于理解
速度慢
存储空间大
循环：
不易理解
速度快
存储空间小

汉诺塔

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


# include <stdio.h>

void hannuota(int n, char A, char B, char C)
{
	/*
	如果是1个盘子
	直接将A柱子上的盘子从A移到C
	否则
	先将A柱子上的n-1个盘子借助C移到B
	直接将A柱子上的盘子从A移到C
	最后将B柱子上的n-1个盘子借助A移到C
	*/
	if (1 == n)
	{
		printf("将编号为%d的盘子直接从%c柱子移到%c柱子\n", n, A, C);
	}
	else
	{
		hannuota(n - 1, A, C, B);
		printf("将编号为%d的盘子直接从%c柱子移到%c柱子\n", n, A, C);
		hannuota(n - 1, B, A, C);
	}
}

int main(void)
{
	char ch1 = 'A';
	char ch2 = 'B';
	char ch3 = 'C';
	int n;

	printf("请输入要移动盘子的个数: ");
	scanf("%d", &n);

	hannuota(n, 'A', 'B', 'C');


	return 0;
}

递归的运用

树和森林就是以递归的方式定义的
树和图的很多算法都是以递归来实现的

很多数学公式就是以递归的方式定义的
斐波拉契序列 1 2 3 5 8 13 21 34 …

非线性结构–树

树的分类：一般树二叉树（一般二叉树，满二叉树，完全二叉树）森林
完全二叉树：如果只是删除了满二叉树最底层最右边的连续若干个节点，这样形成的二叉树就是完全二叉树。满二叉树只是完全二叉树的一个特例。（解决树用数组存储问题连续存储）

二叉树的存储

顺序存储

非线性结构转成线性结构三种方法先中后
优点:查找某个节点的父节点和子节点（也包括判断有没有子节点）方便快速
缺点：耗用内存空间过大

链式存储

两个指针域分别指向两个子节点，没有子节点的为空
优点：耗用内存空间小
缺点：查找父节点不方便

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113


# include <stdio.h>
# include <malloc.h>

struct BTNode
{
	char data;
	struct BTNode * pLchild; //p是指针 L是左  child是孩子
	struct BTNode * pRchild;
};

void PostTraverseBTree(struct BTNode * pT);
struct BTNode * CreateBTree(void);
void PreTraverseBTree(struct BTNode * pT);
void InTraverseBTree(struct BTNode * pT);

int main(void)
{
	struct BTNode * pT = CreateBTree();

	//PreTraverseBTree(pT);
	//InTraverseBTree(pT);
	PostTraverseBTree(pT);

	return 0;
}

void PostTraverseBTree(struct BTNode * pT)
{
	if (NULL != pT)
	{
		if (NULL != pT->pLchild)
		{
			PostTraverseBTree(pT->pLchild);
		}
		if (NULL != pT->pRchild)
		{
			PostTraverseBTree(pT->pRchild);
			//pT->pLchild可以代表整个左子树
		}
		printf("%c\n", pT->data);
	}
}

void InTraverseBTree(struct BTNode * pT)
{
	if (NULL != pT)
	{
		if (NULL != pT->pLchild)
		{
			InTraverseBTree(pT->pLchild);
		}

		printf("%c\n", pT->data);

		if (NULL != pT->pRchild)
		{
			InTraverseBTree(pT->pRchild);
			//pT->pLchild可以代表整个左子树
		}
	}
}

void PreTraverseBTree(struct BTNode * pT)
{
	if (NULL != pT)
	{
		printf("%c\n", pT->data);

		if (NULL != pT->pLchild)
		{
			PreTraverseBTree(pT->pLchild);
		}

		if (NULL != pT->pRchild)
		{
			PreTraverseBTree(pT->pRchild);
			//pT->pLchild可以代表整个左子树
		}
	}

	/*
	伪算法
	先访问根节点
	再先序访问左子树
	再先序访问右子树
	*/
}

struct BTNode * CreateBTree(void)
{
	struct BTNode * pA = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pB = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pC = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pD = (struct BTNode *)malloc(sizeof(struct BTNode));
	struct BTNode * pE = (struct BTNode *)malloc(sizeof(struct BTNode));

	pA->data = 'A';
	pB->data = 'B';
	pC->data = 'C';
	pD->data = 'D';
	pE->data = 'E';

	pA->pLchild = pB;
	pA->pRchild = pC;
	pB->pLchild = pB->pRchild = NULL;
	pC->pLchild = pD;
	pC->pRchild = NULL;
	pD->pLchild = NULL;
	pD->pRchild = pE;
	pE->pLchild = pE->pRchild = NULL;

	return pA;
}

//这是一个二叉树的静态链表存储和遍历实现代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213


#include<stdio.h>
#include<stdlib.h>
#define NULL 0
typedef char TElemType;
//动态二叉链表
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

#define MAXSIZE 100
typedef BiTNode* SElemType;
typedef struct SqStack{
	SElemType data[MAXSIZE];
	int top;//指向栈顶元素
}SqStack;

//初始化空栈
void initStack(SqStack &s){
	s.top = 0;
}

//判栈空
bool isEmpty(SqStack s){
	if (s.top == 0){
		//printf("是空栈\n");//
		return true;
	}
	else{
		return false;
	}
}

//判栈满
bool isFull(SqStack s){
	if (s.top == MAXSIZE){
		return true;
	}
	else{
		return false;
	}
}

//取栈顶元素
void getTopElem(SqStack s, SElemType &e){
	if (!isEmpty(s))
		e = s.data[s.top - 1];
	else
		printf("此栈为空栈，取栈顶元素失败\n");
}

//入栈
void push(SqStack &s, SElemType e){
	if (!isFull(s)){
		s.data[s.top] = e;
		s.top++;
	}
	else
		printf("此栈已满，入栈操作失败\n");
}

//出栈
void pop(SqStack &s, SElemType &e){
	if (!isEmpty(s)){
		e = s.data[s.top - 1];
		s.top--;
	}
	else
		printf("此栈为空栈，出栈操作失败\n");
}

//利用先序序列建立一颗二叉树，先序序列读入：'a', 'b', 'c', '.', '.', 'd', 'e', '.', 'g', '.', '.', 'f', '.', '.', '.' 
//,'.'代表空树
//测试用例：abc..de.g..f...#
void createBiTreeByPreOrder(BiTree &T){
	//按先序次序输入二叉树中节点的值（一个字符），点号字符表示空树，构造二叉链表表示的二叉树
	//注意：若输入的字符数（不含#号）为n个，则相应的空树即点号就应该有n+1个
	char ch;
	scanf_s("%c", &ch);
	//printf("test:%c\n", ch);
	if (ch != '#'){
		if (ch == '.'){
			T = NULL;
		}
		else{
			T = (BiTNode *)malloc(sizeof(BiTNode));
			T->data = ch;
			createBiTreeByPreOrder(T->lchild);
			createBiTreeByPreOrder(T->rchild);
		}
	}
}

//先序遍历打印二叉树的递归算法(根、左、右)
void preOrderPrint(BiTree T){
	if (T){
		printf("%c ", T->data);
		preOrderPrint(T->lchild);
		preOrderPrint(T->rchild);
	}
}

//先序遍历打印二叉树的非递归算法(根、左、右)
void preOrderPrint2(BiTree T){
	SqStack s;
	initStack(s);
	BiTNode *p = T;
	while (p || !isEmpty(s)){
		if (p){
			printf("%c ", p->data);
			push(s, p);
			p = p->lchild;
		}
		else{
			//printStack(s);
			pop(s, p);//栈顶指针（当前层的根节点指针）弹出
			p = p->rchild;
		}
	}
}

//中序遍历打印二叉树的递归算法（左、根、右）
void inOrderPrint(BiTree T){
	if (T){
		inOrderPrint(T->lchild);
		printf("%c ", T->data);
		inOrderPrint(T->rchild);
	}
}
//中序遍历打印二叉树的非递归算法（左、根、右）
void inOrderPrint2(BiTree T){
	SqStack s;
	initStack(s);
	BiTNode *p = T;
	while (p || !isEmpty(s)){
		if (p){
			push(s, p);
			p = p->lchild;
		}
		else{
			pop(s, p);//栈顶指针（当前层的根节点指针）弹出
			printf("%c ", p->data);
			p = p->rchild;
		}
	}
}

//后序遍历打印二叉树的递归算法（左、右、根）
void postOrderPrint(BiTree T){
	if (T){
		postOrderPrint(T->lchild);
		postOrderPrint(T->rchild);
		printf("%c ", T->data);
	}
}
//后序遍历打印二叉树的非递归算法（左、右、根）
void postOrderPrint2(BiTree T){
	SqStack s;
	initStack(s);
	BiTNode *p = T;
	while (p || !isEmpty(s)){
		if (p){
			push(s, p);
			p = p->lchild;
		}
		else{
			BiTNode *top;
			getTopElem(s, top);//取得栈顶元素
			if (top->data > 0){//栈顶元素的右子树还没有被访问过
				p = top->rchild;
				top->data = -top->data;//赋右子树已遍历标志

			}
			else{//栈顶元素的右子树已经访问过了
				printf("%c ", -top->data);
				pop(s, top);
				//p = NULL;				
			}
		}
	}
}

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以点号表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	printf("先序遍历打印二叉树:\n");
	preOrderPrint(T);
	printf("\n");

	printf("先序遍历打印二叉树（非递归算法）:\n");
	preOrderPrint2(T);
	printf("\n");

	printf("中序遍历打印二叉树:\n");
	inOrderPrint(T);
	printf("\n");

	printf("中序遍历打印二叉树（非递归算法）:\n");
	inOrderPrint2(T);
	printf("\n");

	printf("后序遍历打印二叉树:\n");
	postOrderPrint(T);
	printf("\n");

	printf("后序遍历打印二叉树（非递归算法）:\n");
	postOrderPrint2(T);
	printf("\n");

	
}

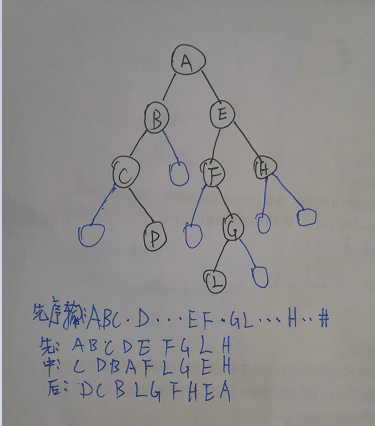
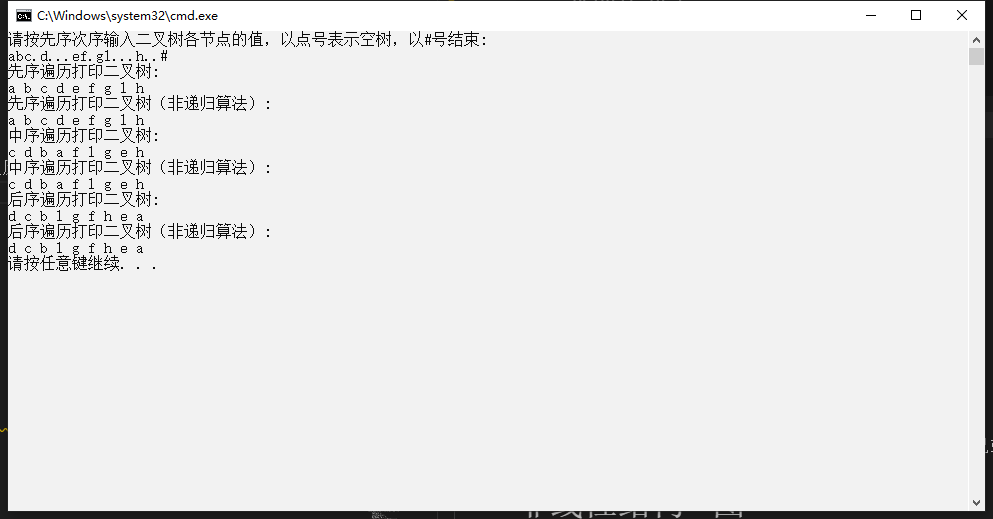
这是一个二叉树的动态链表存储和遍历的代码

测试用例子
二叉树

一般树的存储

普通树转换为二叉树
左指针域指向它的第一个孩子
右指针域指向它的下一个兄弟

森林存储

森林转化为二叉树
将森林中的每个树的节点当做兄弟存储
左指针域指向它的第一个孩子右指针域指向它的下一个兄弟

非线性结构–图

查找和排序

排序：冒泡插入选择快速归并
查找：排序是查找的前提

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


# include <stdio.h>

int FindPos(int * a, int low, int high);
void QuickSort(int * a, int low, int high);
int a[100], n,i;
int main(void)
{
	printf("请输入要排序数字的总数：");
	scanf_s("%d", &n);
	for (i = 0; i < n;i++)
	{
		printf("数据：");
		scanf_s("%d", &a[i]);
	}
	
	

	QuickSort(a, 0, n-1); //第二个参数表示第一个元素的下标  第三个参数表示最后一个元素的下标
	printf("排序如下：\n");
	for (i = 0; i < n; ++i)
		printf("%d  ", a[i]);
	printf("\n");

	return 0;
}

void QuickSort(int * a, int low, int high)
{
	int pos;

	if (low < high)
	{
		pos = FindPos(a, low, high);
		QuickSort(a, low, pos - 1);
		QuickSort(a, pos + 1, high);
	}
}

int FindPos(int * a, int low, int high)
{
	int val = a[low];

	while (low < high)
	{
		while (low < high  && a[high] >= val)
			--high;
		a[low] = a[high];

		while (low < high && a[low] <= val)
			++low;
		a[high] = a[low];
	}//终止while循环之后low和high一定是相等的

	a[low] = val;

	return high; //high可以改为low, 但不能改为val 也不能改为a[low]  也不能改为a[high]
}

快速排序源代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


# include <stdio.h>

//冒泡排序
void sort(int * a, int len)
{
	int i, j, t;

	for (i = 0; i < len - 1; ++i)//整体比的次数 比一次就会找到一个最大值 所以比的次数为元素个数减一
	{
		for (j = 0; j < len - 1 - i; ++j)//len-1-i 代表还没比出来的最大元素也就是前面几个元素比
		{
			if (a[j] > a[j + 1])  // >表示升序 <表示降序
			{
				t = a[j];
				a[j] = a[j + 1];
				a[j + 1] = t;
			}
		}
	}
}

int main(void)
{
	int a[6] = { 10, 2, 8, -8, 11, 0 };
	int i = 0;

	sort(a, 6);

	for (i = 0; i < 6; ++i)
	{
		printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

冒泡排序

排序算法比较与梳理

泛型

到底什么是泛型：
同一种逻辑结构，无论该逻辑结构物理存储是什么样子的我们都可以对它执行相同的操作（例如都是线性结构或者用数组实现的树和用链表实现的树。利用重载技术。）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


#include <stdio.h>
int a[10], book[10], n;
void dfs(int step)
{
	int i;
	if (step == n + 1)
	{
		for (i = 1; i <= n; i++)
			printf("%d", a[i]);
		printf("\n");
		return;
	}
	for (i = 1; i <= n; i++)
	{
		if (book[i]==0)
		{
			a[step] = i;
			book[i] = 1;
			dfs(step + 1);
			book[i] = 0;
		}
	}
	return;
}
int main()
{
	scanf_s("%d", &n);
	dfs(1);
	getchar();
	getchar();
	return 0;
}

深度优先搜索

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


#include <stdio.h>
int a[10], book[10], total=0;
void dfs(int step)
{
	int i;
	if (step ==10)
	{
		if (a[1]*100+a[2]*10+a[3]+a[4]*100+a[5]*10+a[6]==a[7]*100+a[8]*10+a[9])
		{
			total++;
			printf("%d%d%d+%d%d%d=%d%d%d", a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8], a[9]);
			printf("\n");
		}
		return;
	}
	for (i = 1; i <= 9; i++)
	{
		if (book[i]==0)
		{
			a[step] = i;
			book[i] = 1;
			dfs(step + 1);
			book[i] = 0;
		}
	}
	return;
}
int main()
{
	
	dfs(1);
	printf("total=%d", total / 2);
	getchar();
	getchar();
	return 0;
}

数据结构与算法笔记

文章目录

数据结构概述

算法概述

指针

结构体

动态分配内存

线性结构表

顺序存储 [数组]

链式存储 [链表]

线性结构的应用–栈

静态栈

动态栈（重点）

线性结构的应用–队列

动态队列

静态队列（重点）

递归

递归的运用

非线性结构–树

二叉树的存储

顺序存储

链式存储

一般树的存储

森林存储

非线性结构–图

查找和排序

泛型

文章目录

数据结构概述

算法概述

指针

结构体

动态分配内存

线性结构 表

顺序存储 [数组]

链式存储 [链表]

线性结构的应用–栈

静态栈

动态栈（重点）

线性结构的应用–队列

动态队列

静态队列（重点）

递归

递归的运用

非线性结构–树

二叉树的存储

顺序存储

链式存储

一般树的存储

森林存储

非线性结构–图

查找和排序

泛型

线性结构表